Can I safely see Grandma?
Grandma has gotten her COVID-19 vaccine and is a few weeks out from the second shot in the series. Now everyone wants to know: can I safely see my Grandma?
The New York Times says it is probably safe but should be done outside and with masks. Experts elsewhere have stressed the importance of avoiding contact with the elderly, masking, and social distancing if you do have visits after vaccination (see, these, examples).
While some experts are more risk accepting in their guidance, they aren’t able to give a “definitive” answer. Even with a vaccine and other efforts like pre-visit isolation, there is always the risk of spreading COVID-19 to Grandma. Therefore, the preference is to err on the side of caution. We don’t know how safe a visit is but we do know it is less safe than no visit. Therefore, the recommendation is either no or extremely limited visits.
We see the same thing in advice to pregnant women. Alcohol consumption while pregnant clearly and indisputably can cause harm to the fetus, including loss of pregnancy and development complications. But increasingly, it seems like there is some amount of alcohol that can be consumed without harm. A meta-analysis pooling data from several other studies found no evidence of a harmful effect at $\leq$ 1 drink per day. But we cannot know that drinking up to 1 drink per day is safe without doing a randomized trial. It wouldn’t be ethical to tell some pregnant women to drink - we know alcohol is bad - and so we can’t find the “safe dose.” It is safer not to drink at all than to risk drinking more than the unknown safe dose and, given the potential risks of exceeding the safe dose, guidelines say “don’t drink when pregnant.”
The same logic is being applied here. While asking someone to give up drinking alcohol for a few months is somewhat low cost, asking Grandma to give up time with her grandchildren is a harder request. The social interaction is important for both the grandchildren and grandparents and the COVID-19 pandemic has increased already high high levels of isolation for the elderly. It isn’t clear that the costs of giving up grandchildren time is as easily dismissed as the costs of giving up alcohol for a few months.
Instead, it might be better to think about whether we can safely see Grandma in terms of the expected costs and expected benefits of the visit. Specifically, I am thinking of the expected costs - the marginal increase in risk to Grandma - resulting from a visit and how that risk compares to risks we more routinely assume.
I start by picturing a model of our question:
graph TD
A[You] -->|1-Pi| B[Not Infected]
B -->|100%| C(No Risk to Grandma)
A -->|Pi| D[Infected]
D -->|Pt| E(Infect Grandma)
D -->|1 - Pt| F(Don't Infect Grandma)
You go visit Grandma. Either you aren’t infected, in which case Grandma is totally
fine or you are infected and the risk to Grandma depends on the transmission risk.
Those values are denoted in the graph with Pi being the risk that you - or another
visitor - is infected and Pt being the risk that transmission occurs between an
infected visitor and Grandma.
Based on this model, if we know the value of Pi and we know the value of Pt,
we can compute the risk to Grandma for a visit.
How Likely is an Infected Guest
We first need to know how many people in a community are infected. This gives us a pretty good estimate of the probability a randomly selected member of the community is infected. To start with, we could use the 14-day moving average of incidence per 100,000 as reported for your county on COVIDActNow. For my county, that is about 15-20 new cases per day per 100,000 people.
Next, we need to increase this to find the total number of infectious people in the county. If we assume people are infectious, on average, for 10 days, we could simply multiply the daily incidence by 10 to get a reasonable estimate. For my county, we would be looking at 150 to 200 people per 100,000 that are infectious. We would then express the probability a randomly selected person has infectious COVID19 as
$$ \Pr(\text{Infected}) = 10 r $$
where $r$ is the rate of new cases per day.
Many people with COVID19 have very limited or even no symptoms and, as such, are unlikely to seek out testing. To account for that, we would need to divide the observed $r$ by the fraction (let’s call it $\phi$) that we think does show symptoms. Then
$$ \Pr(\text{Infected}) = \frac{10r}{\phi} $$
In other words, if we have $r = 15$ and we think only 70% of people with COVID19 have symptoms, we would expect the true number of infected people per 100,000 to be $\frac{10 \cdot 15}{0.7} = 214.3$.
Ways to Reduce the Risk of Being Infected
The simplest way to reduce the risk of being infected is to self-isolate for several days before visiting Grandma. This prevents you from getting infected during those days and adds a “buffer” period between your last exposure and your visit for any infection to become apparent. I assume the incubation period of COVID is distributed log normal with a mean of 1.5 and a standard deviation of 0.5 Our expected incubation period would look like:
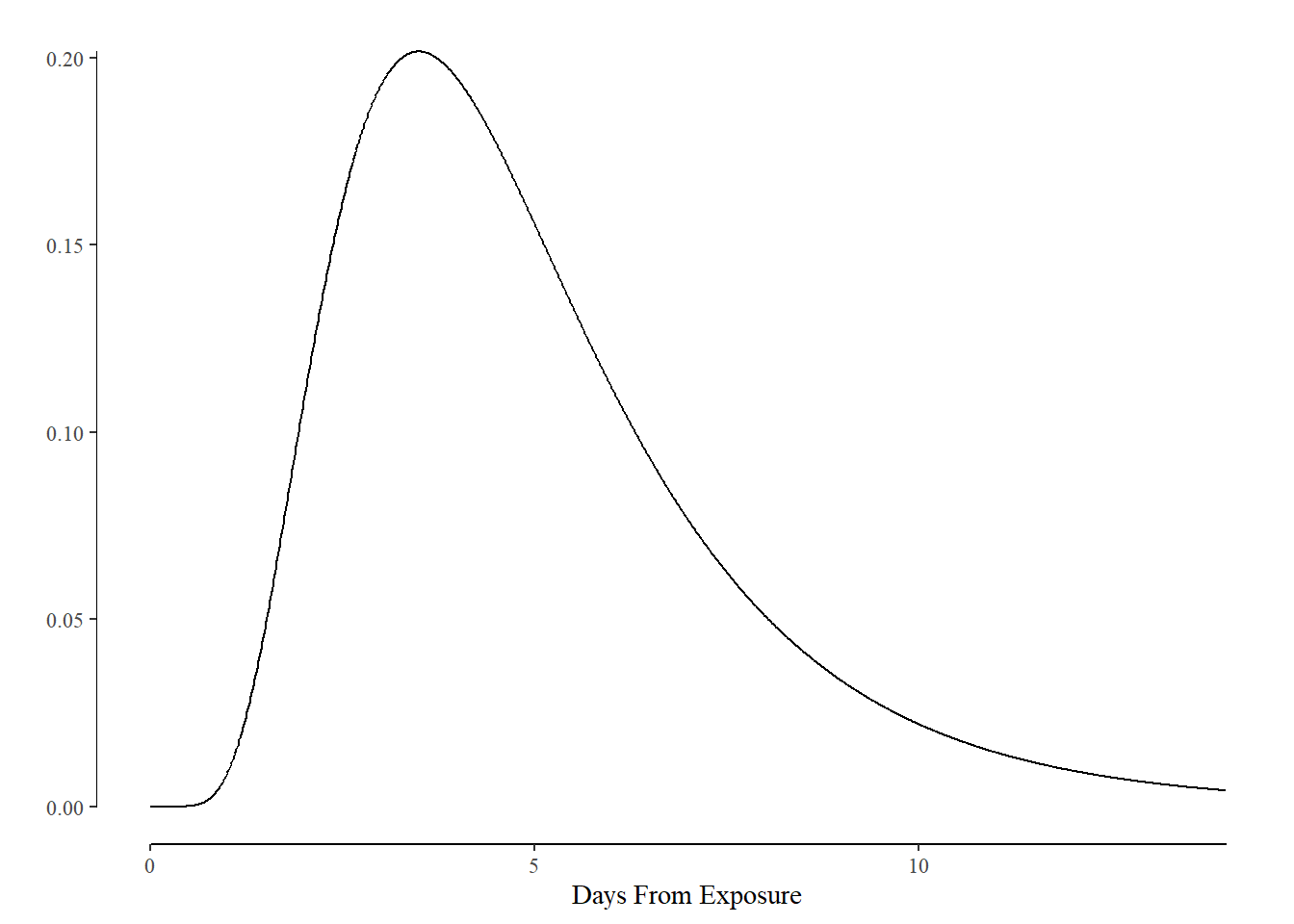
An advantage of using a distribution like the log normal is that we then can calculate the probability that someone is not infection based on the duration of their isolation without having symptoms. Specifically, the value $1 - \text{CDF}(q)$, where $q$ is the number of days in isolation and $\text{CDF}$ is the cumulative density function, gives us the tools we need to modify the baseline probability of infection:
$$ \Pr(\text{Infected} | Q = q) = \bigg(1 - \text{CDF}(q)\bigg) \frac{10r}{\phi} $$
Of course, a person who is infected and asymptomatic will not be caught through this scheme. Therefore we need to add a slight tweak where we allow for $1 - \phi$ people to pass isolation without detection.
$$ \Pr(\text{Infected} | Q = q) = \bigg[\phi \bigg(1 - \text{CDF}(q)\bigg) + (1 - \phi)\bigg]\frac{10r}{\phi} $$
This allows $1 - \phi$% people to pass through isolation without symptoms but detect $\phi$% of cases.
What is the Probability of Transmission
I base the model for transmission between an infected person and an non-infected person exactly on the model used by the MicroCOVID Project. Specifically,
- there is a 9% per hour per infected person risk of transmission at baseline
- Grandma wearing a mask reduces her risk by 50%
- guests wearing masks reduces Grandma’s risk by 75%
- being outside reduces risk by 95%
- being more than 6 feet apart reduces risk by 50%
- vaccines reduce risk by $1-VE$%, where VE is the vaccine efficacy
The transmission risk is the product of the interventions. For instance, the risk of transmission per hour spend outside and without masks is
$$ \Pr(\text{Transmission}) = 0.09 \cdot 0.05 $$
or 0.45% per hour.
Putting these models together
We assume transmission and infection probabilities are independent. Then the joint probability - the probability that someone is present, infectious, and transmits the virus - is the product of the two probabilities. We have a transmission opportunity each hour for each guest (e.g., two guests for four hours is 8 opportunities). We then assume the number times times that Grandma is exposed to an infectious dose is distributed
$$ B(\text{guests}\cdot\text{duration}, \Pr(\text{infected})\cdot\Pr(\text{transmission} | \text{infected})) $$
Then the probability of having a random draw from that distribution exceeding zero is the probability of grandma being infected.
(This is a pretty basic model. For starters it assumes guests and time are the same. One guest for 24 hours or 24 guests for 1 hour are the same risk. However, it is 23.4 times more likely that 1 or more of the 24 guests will be infected than the 1 guest. These obviously are not the same; however, a simple model can still be useful.)
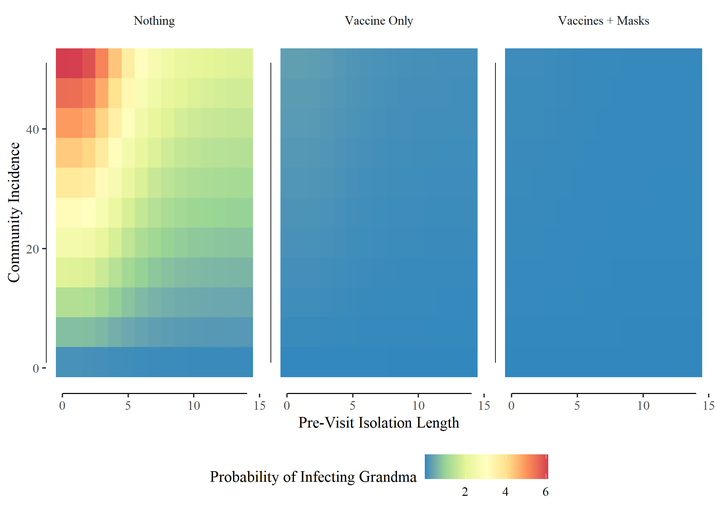
Based on these two sets of assumptions, we can estimate the probability of transmission from a guest to Grandma for any event Grandma might want to hold. Let’s assume the event is a gathering of 4 people and they are staying for 24-hours - your classic Grandparent overnight visit.
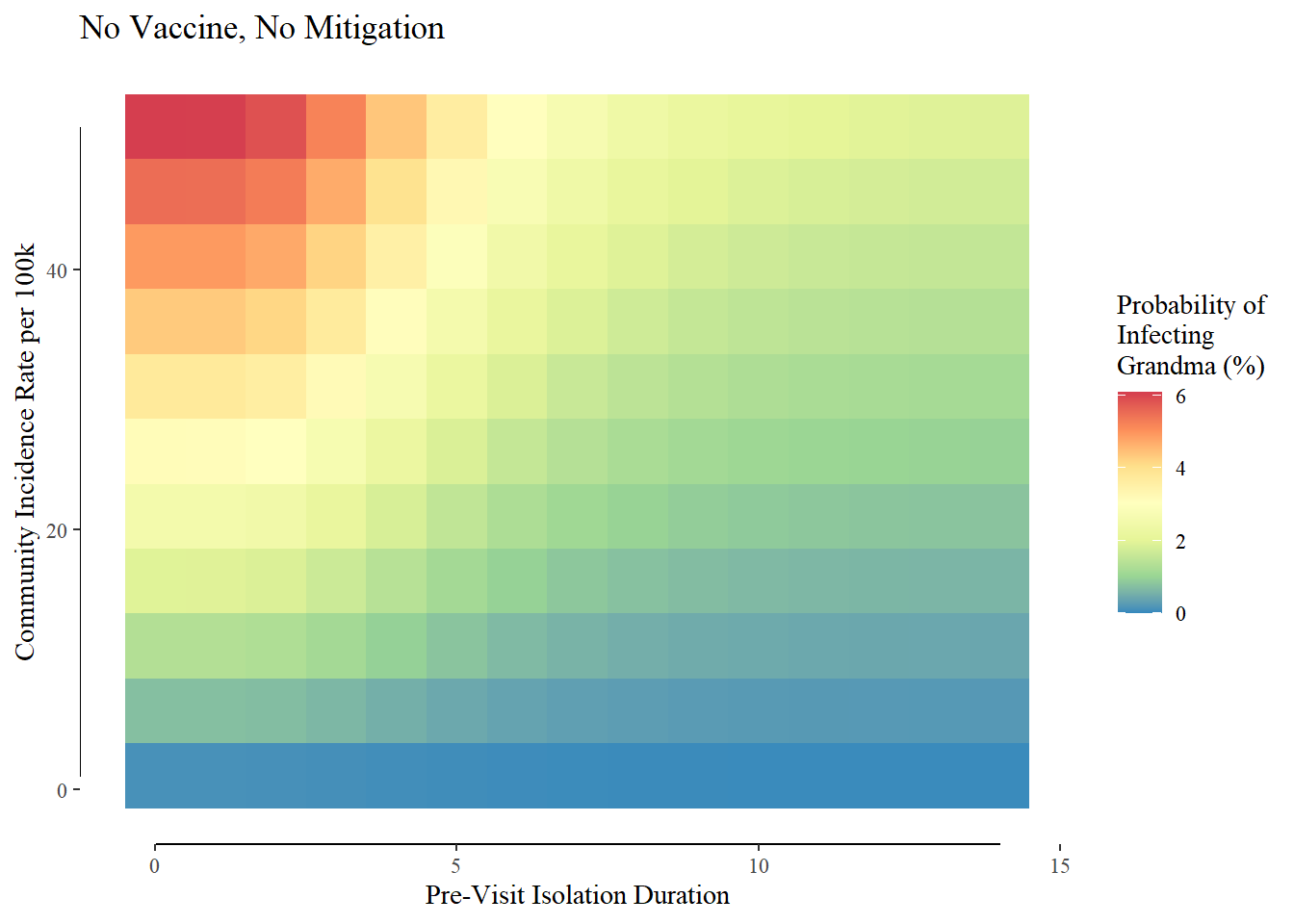
We start by considering several combinations community incidence (1 to 51 cases per day per 100,000) and isolation periods (0 to 14 days). I assume $\phi = 0.7$.
Visiting Grandma before her vaccine and with no mitigation measures would have been a bad idea:
But the vaccine (VE =95%, the number reported in the trials of both the Pfizer and Moderna mRNA vaccine candidates and supported by “real-world” evidence from Israel) is a game changer:
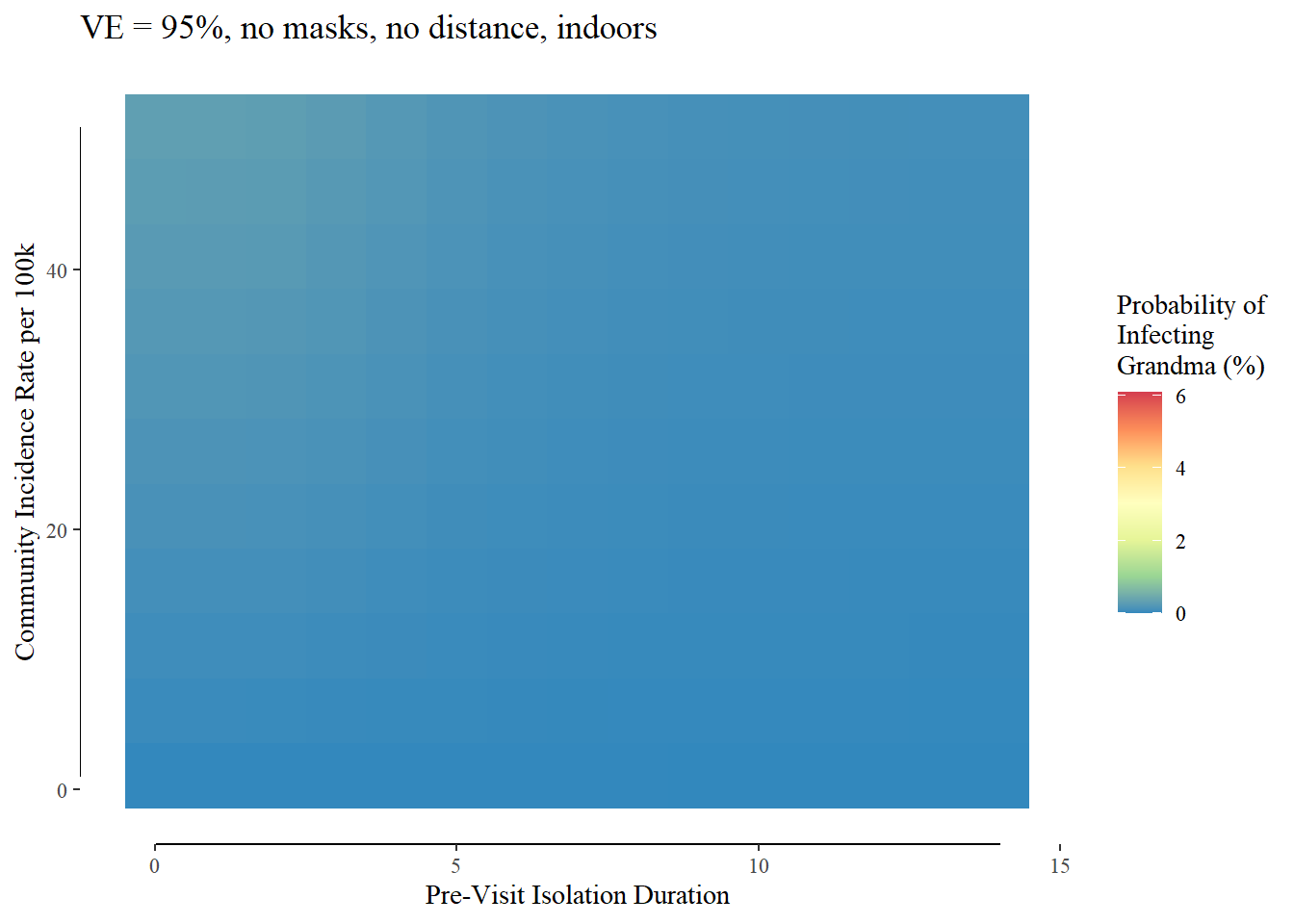
Additional interventions reduce the risk even more with the most extreme - masks, outdoors, and distanced being functionally zero:
To focus on my specific county (15.2 cases per 100,000 over the last 14 days), a plausible isolation period (3 days), 3 guests (my wife, my daughter, myself), and a 24-hour stay:
| Probability Grandma Gets Infected | |
|---|---|
| Baseline | 1.192% |
| Vaccine | 0.060% |
| Vaccine + Masks | 0.007% |
| Vaccine + Masks + Distance | 0.004% |
| Vaccine + Masks + Distance + Outdoors | 0.000% |
The vaccine alone is extremely effective, taking the risk of our visit infecting grandma from 1.19% to 0.06%. Other mitigation efforts reduce it further; although, considering what I know about Grandma, masking would likely be the only practicable addition.
Putting Numbers in Context
So there is a 0.06% chance of my visit infecting Grandma if she’s been vaccinated and we do nothing else. Is this a high number? A low number? How can I evaluate this risk against something I already implicitly accept?
One useful benchmark is against driving. In the United States, there are, on average, 1.15 fatalities per 100,000,000 miles driven. We can convert the expected risk of infection and age-adjusted risk of death to the number of miles of driving that would be equal risk.
To figure this number out, we need to compute the expected risk of death following infection. Using data from this meta-analysis it seems like the risk of death from COVID19 infection is
$$ \Pr(\text{Death} | \text{Infected}) = \frac{10^{-3.309392 + 0.052486 \cdot \text{age}}}{100} $$
For our case study, Grandma is 65, Grandpa is 75. The risk of infection is 0.18% and the risk of death for Grandma, if infected, is 1.26% and 4.24% for Grandpa. The probability of the visit causing Grandma’s death is 0.0008% for Grandma and 0.0025% for Grandpa. Using the death per mile figure, that is equal to driving about 660 for Grandma and about 2,210 miles for Grandpa.
A visit to see Grandma, for us, is about 400 miles round trip. The risk of the drive causing a fatalities is 60% as large as the risk to Grandma. We easily and routinely accept that risk. The risk to Grandpa is larger due to his greater risk of mortality but it is still small - roughly the distance of a round trip drive to New York City or Philly (something we’ve done several times) or the amount of driving done in 2 months for the average American (13,500 miles per year).
My take on those numbers - and the distances that provide anchors to known risks - is that the risk of seeing Grandma or Grandpa at our current levels of incidence, after a brief period of isolation, and at least 2 weeks after both Grandma and Grandpa have been vaccinated might be acceptable even without masks, gathering indoors, and without any social distancing. The risks are comparable to ones we routinely take. However, the risk to Grandpa, in particular, could add up fast if we made frequent visits to see the grandparents. One visit is probably within our normal risk threshold, but weekly visits are likely not.
Everything is a Trade-Offs
Everything has risk and costs. Here I’ve focused on estimating the risk of COVID transmission or death resulting from a visit to a loved one. We can be safer by not seeing these loved ones right now and instead waiting 3? 6? 9? months until the situation has improved. And for some people, that might be the best choice. But for grandparents who’ve already lost a year of precious, irreplaceable time with their grandchildren, it might not be the right choice. By thinking explicitly about the trade-offs, it might be possible to make better decisions.
Appendix: Want to calculate your own risk?
I did the simulations above in R. Below is an R function for you to run to find the risk given any infection rate, pre-visit isolation, and mitigation efforts. Also allow for varying the infectious of the virus, as may be occurring with new variants emerging in the UK and South Africa.
risk_bringing_covid <- function(infection_rate, q_duration,
num_guests, hours,
ve, mask, outdoors, distance,
phi = 0.7, theta = 1) {
# infection rate is new cases per 100,000 per day (e.g., the number from COVID Act Now)
# q_duration is the number of days of pre-visit isolation
# num_guests are how many people are visiting Grandma
# hours is duration of the visit
# ve should be the vaccine efficacy (0% VE is the same as no vaccine)
# RCTs for the mRNA vaccines are 0.95 in both RCTs and observational studies
# this might decrease with the emergence of new variants but VE >0.7 seems
# like a reasonable safe assumption
# mask, outdoors, distance should be 1 if in effect, 0 o/w
# phi is the adjustment for asymp. carriers and is equal to % that show symptoms
# this isn't certain by values of 0.5 to 0.8 are reasonable
# theta is a parameter to make the transmission more likely (e.g., as with new variants)
# defaults to 1.00, 1.50 would be 50% more infectious
pr_infected <- 10 * infection_rate / 100000 / phi *
(phi * plnorm(q_duration, 1.5, 0.5, lower.tail = FALSE) + (1 - phi))
risk_reduction <- (1 - ve) *
ifelse(mask, 0.25 * 0.5, 1) *
ifelse(outdoors, 0.05, 1) *
ifelse(distance, 0.5, 1)
transmission_risk <- theta * 0.09 * risk_reduction
# take the probability of infection * transmission risk to get the joint prob
# then it is simply a binomial distribution problem
# this returns the prob that exactly 0 transmission events occur
pr_grandma <- pbinom(0, num_guests * hours, pr_infected * transmission_risk,
lower.tail = FALSE)
return(pr_grandma)
}